2012-11-10 | 编辑：文\先进制造研究部 

先进制造研究部于丹、李晓冬和庹睿等最近在表征纳米复合材料中纳米粒子的分散程度方面取得进展。

纳米复合材料是否具有优良特性与材料中加入的纳米粒子在基材中的分散情况息息相关。对于纳米复合材料中纳米粒子分散度的量化表达是对纳米复合材料进行质量控制进而实现大规模生产的基础，所以是纳米复合材料领域的共性问题。

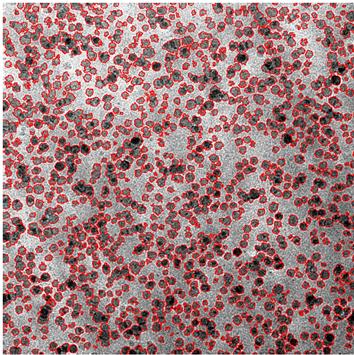
透射电镜（TEM）可以用来拍摄纳米材料中粒子的分布情况，是最常用的评估纳米材料分散情况的媒介。透射电镜输出1024×1024像素的灰度图片。找出纳米粒子在图片中的位置是量化分散情况的基础。最近于丹和李晓冬，与澳大利亚昆士兰理工大学的黄大威教授共同提出了统计聚类方法用于区分图片中的两类像素： 黑（粒子）和白（背景）。由于图片中信噪比比较差，在聚类过程中采用了三种方法以提高准确率： 1）采用自适应混合高斯聚类方法，使得待聚类像素的类别信息依赖于其二维空间中邻域的灰度强度，从而减少粒子中白像素个数和背景中黑像素个数。2）照相镜头长时间使用产生的油污或者照相过程中系统其他因素（如未进行校准）可以造成在图片局部区域过黑的现象，从而造成系统误差。应用待聚类像素与其二维空间中邻域像素的均值的差值来进行聚类，可以校正偏差。3） 二分类聚类方法可能不适用于对比度不均匀的图片，因此他们提出应用回归树对图像进行区域划分，然后再进行聚类的方法。应用上述三种方法，他们实现了对100纳米至500纳米标尺的图像的二分类，从而成功的找出纳米粒子团的边缘（见图）。

于丹、李晓冬和美国密歇根大学的金炯华教授合作开展了提取分散度特征量以及特征量应用的研究，实现了TEM图像处理。他们应用统计仿真试验来模拟大小均匀的球形纳米粒子在三维空间中的分布，从而研究三维材料投影到二维TEM图像后分散度的代表性问题。首先他们确定了纳米粒子在三维空间中的理想分散状态，即统计假设检验的零假设。在关于纳米粒子二维分布的研究中，零假设一般设定为空间随机分布。三维的空间随机分布投影到二维，依然是二维空间的随机分布。但是由于很多待研究纳米粒子为刚性物质，在三维空间中互不重叠，因此纳米粒子在三维空间中的分布要受到粒子间间距不小于两个粒子半径的限制，称之为“hardcore”。他们把“hardcore”限制下的空间随机分布设为零假设，开展关于识别纳米粒子聚团的假设检验研究。这个零假设更贴近于实际情况，并与传统的空间随机分布零假设可能存在两方面的差异。第一,在实际操作中，材料中加入的纳米粒子体积比为固定值，比如3％、10％等等。也就是说，宏观材料中的纳米粒子个数基本是固定的。由于这些固定个数的粒子在材料中的空间分布是随机的，在照相区域中的粒子个数就是一个随机变量。如果没有“hardcore”限制，照相区域中的粒子个数近似为泊松分布。有了“hardcore”的限制，照相区域中的粒子个数的分布尤其在粒子体积比比较大的情况下可能会偏离泊松分布。第二,即使粒子个数的分布相同，粒子在空间中的分布也会因为“hardcore”限制而比空间随机分布显得更有规律性，从而造成各种分散度指标的差异。照相区域中的粒子个数分布因为涉及到多重积分而很难理论推导，而宏观材料中粒子的分布又因为粒子个数超出计算机处理范围而无法直接模拟，因此仿真计算面临巨大的挑战。据此，庹睿提出应用随机逼近蒙特卡罗方法来模拟三维空间“hardcore”限制下的随机分布，成功解决了计算方面的难题。