多个体系统由相互作用多个个体构成，在物理、生态、政治和社会经济领域无处不在。例如，小到等离子体、声子、菌落，大到鱼群、鸟群、人群，再大到经济系统、社会系统、天体系统，都可以视为多个体系统。多个体系统经常涌现出各种具有规律的宏观现象，称之为集体行为，如超导、漩涡、同步、人群恐慌、经济危机等。具有局部相互作用的微观个体如何导致宏观系统的集体行为，是系统学研究最基本的科学问题之一。

为了更好理解非平衡系统的分簇、传递和相变等行为， T.Vicsek等人(Phys. Rev. Lett.,1995)提出了一类著名的自驱动粒子（Self-Propelled Particle, SPP)模型（又被称为Vicsek模型）：假设n个个体在平面上运动，其位置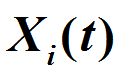和角度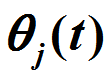的更新方程如下：

 

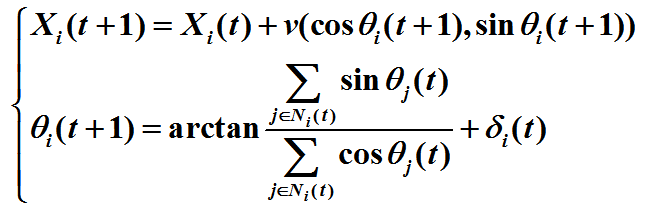
其中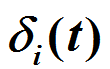表示环境噪声。该模型规则简单但不失本质，抓住了许多系统共性，有助于理解局部规则如何导致系统整体行为，吸引了不同领域学者包括兴趣（目前该论文被引用超过3000次，google数据）。例如，多位著名生物学家如William Bialek（美国国家科学院院士）、Simon A. Levin（美国国家科学院院士）均采纳或引用该模型用于研究生物群体运动。然而，该模型涉及非线性、非平衡性、强耦合性和动态性，尚无成熟理论工具严格分析。事实上，物理学家对该类远离平衡态系统也缺乏成熟工具分析，只能用平均场方法、流体力学方程等作近似处理但结果很不精确。数学上，对该模型主要有如下两种近似处理方式：一种是A.Jadbabaie等人将其角度更新方程线性化并忽略噪声的影响，称之为线性化Vicsek模型；另一种是F.Cucker和S.Smale(菲尔兹奖和沃尔夫奖获得者，美国国家科学院院士）将局部相互作用方式修改为全局相互作用方式，称之为Cucker-Smale模型。这两种近似方式均产生了很大影响，例如，A.Jadbabaie等人论文获IEEE George S. Axelby最佳论文奖，Seung-Yeal Ha在2014年世界数学家大会上报告了他在Cucker-Smale模型方面的研究成果。

对于线性化Vicsek模型，A.Jadbabaie等人证明了当节点构成的加权邻接图满足联合连通条件时, 系统将会同步。但该假设难以验证。G.G.Tang和L.Guo提出了一个随机框架，即假设所有个体的初始位置服从某种概率分布。在该框架下，他们给出了仅依赖初始状态和系统参数的同步条件。后来，Z.X.Liu和L.Guo等人有了重要进展，然而有一个悬而未决的问题是：系统能同步的最小交互半径是多少？

信息技术部的陈鸽与合作者利用渗流理论对临界连通半径之上的随机几何图所对应平均矩阵的谱隙给出了紧致的理论结果，得到了线性化Vicsek模型同步条件的一个关于交互半径的临界结果：当个体间的交互半径高于临界连通半径时，如果速度满足一定条件，那么系统渐近以概率1对任意初始角度都同步；当交互半径低于临界连通半径时，对任意大的速度，系统都渐近以概率1存在某些初始角度使得最终不同步。因此在某种程度上解决了随机框架下线性化Vicsek模型同步充分条件中交互半径的下限问题。该论文首次发表于SIAM Journal on Control and Optimization,Vol.50, 2012，并被美国SIAM Review期刊评选为“SIGEST论文”重新发表于 2014年第3期。SIAM Review是美国工业与应用数学学会（SIAM）的旗舰刊物，它每年从SIAM十多个专业子刊中选出四篇“SIGEST论文”，其目的是使更多读者关注近期发表在SIAM各专业刊物中具有“普遍兴趣的杰出论文（outstanding paper of general interest）”。该文入选的理由是“贡献和研究问题的重要性，论文写作的清晰性，以及SIAM领域的相关性（the importance of its contributions and topic, its clear writing style, and its accessibility for the SIAM community）”SIAM将“SIGEST论文”视为一项奖励，证书将在2015年的SIAM 授奖仪式上颁发。这是中国大陆学者首次获该项荣誉。

噪声对秩序的影响是物理学家、生物学家和化学家一直关心的问题。Vicsek模型被提出时，就通过仿真研究了噪声、次序与个体密度之间的一些相变关系(Phys. Rev. Lett.,1995)；Buhl 等人(Science,2006)利用Vicsek模型在模拟沙漠蝗虫（图1）集体运动时发现：给定噪声，如果蝗虫密度很高，系统的很快处于高度有序的状态；如果密度很低或中等时，系统将会涌现群体变向并且序参数剧烈波动（图2）。T. Shinbrot和F. Muzzio（Nature, 2001）则研究了在一些物理现象例如热波动和机械随机散射中噪声对秩序的促进作用以及背后机制。然而，这些研究仍停留在物理上近似分析以及模拟阶段，在数学上几乎没有任何结果。信息技术部的科研人员最近在该模型上取得了一系列进展，研究意义如下：

数学：提出了一套解耦半确定半随机非线性系统新方法。利用该方法首次给出了原始Vicsek模型严格分析结果，并对一些非齐次SPP模型包括Leader-follow模型也得出一些分析结果；解决了A.Jadbabaie等人在论文中所提噪声如何影响连通性问题；针对很多文献所关心的“鲁棒同步”问题给出了一个明确答案。

物理：揭示了局部规则如何导致系统整体行为，证明了对任意大的密度和任意小的噪声SPP系统将会在有序与无序之间切换无穷次。该结果说明小噪声能破坏系统秩序，于是严格验证了统计物理学界“噪声能对远离平衡态系统全局行为造成极大波动”这一观点；同时也说明了Vicsek模型的秩序关于密度与噪声的相变关系不是传统方式，并推测该模型相变存在新的形式。

生物：数学上证明了噪声能导致生物集群的转向、分簇、汇聚等行为；一定程度上解释了J.Buhl 等人(Science,2006)在蝗虫实验中非高密度时群体变向和序参数剧烈波动现象，并预测高密度时如果时间足够这些现象仍将发生。

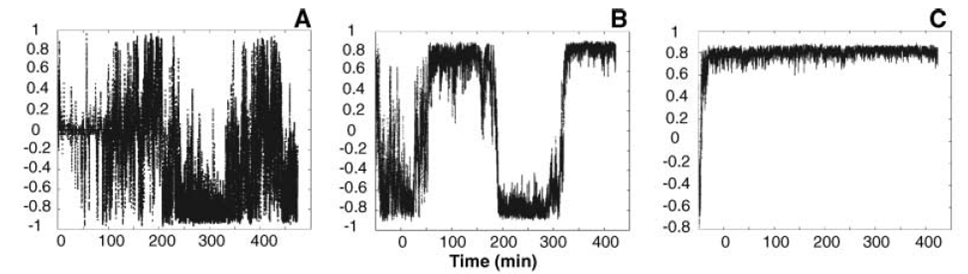图1：沙漠蝗虫队列（图片来自http://www.sciencemag.org/content/ 312/5778/1320/F1.expansion.html)		图2：序参数演化图（A、B、C分别分别代表低、中、高密度，图片来自J.Buhl et al.,Science,2006）