基于数学模型的计算机实验是科学工作者了解复杂物理系统的有力工具。给定了若干输入值后,计算机实验会通过计算得到若干输出值。对于计算时间较长的计算机实验,需要通过统计实验设计的方法,减少实验次数,节省时间。由于同样的输入值会导致同样的输出值,针对计算机实验的设计有别于传统的实验方法。计算机实验设计的一个核心问题是优化。即,找到最佳的输入值,使得计算机实验的输出值尽量小。本工作的主题就是通过序贯设计的方法进行计算机实验寻优。
通常而言,计算机实验是对数学模型的近似。许多计算机实验的近似精度可以通过精度参数控制。比如,金属铸造领域的计算机实验是对金属液体在模具中流动、冷却、凝固过程的模拟。模拟需要使用有限元方法,即将铸件依据空间位置切成大量的小方格,以便于计算。方格划分越细,计算精度越高,计算时间越长。此时方格的边长就是精度参数。而这个精度参数是可控的。
传统的计算机实验寻优方法使用固定精度的计算机实验。这样做有几个缺点。一是如果精度参数选择得不好,则事倍功半。二是随着实验不断深入,计算机实验的精度理应提升。我们提出一套使用多种精度计算机实验的方法。首先使用三分之一左右的时间进行摸底实验。摸底实验的实验点要求在空间中均匀分布,并使用较低的精度值。剩余三分之二的时间进行追加实验,追加实验集中在输出值较小的区域,分两种类型,包括精细搜索,即在已知较优的区域加作实验,以及全局探索,即在不确定性大的区域加作实验。追加实验的精度总体应高于摸底实验,且精细搜索的精度应高于全局探索。
具体地,我们使用一个非平稳的高斯过程模型来进行计算机建模。该模型将精度参数作为一个连续、非平稳的参数,可以综合多精度信息建模。我们关心的响应,是所谓精确解,即方格直径无限小时的输出值。我们发展了传统的预期提高判据(EI),得到了预期分位数提高判据(EQI)及预期分位数提高效率判据(EQIE),并用这些判别来指导追加实验的输入值及精度参数选取。
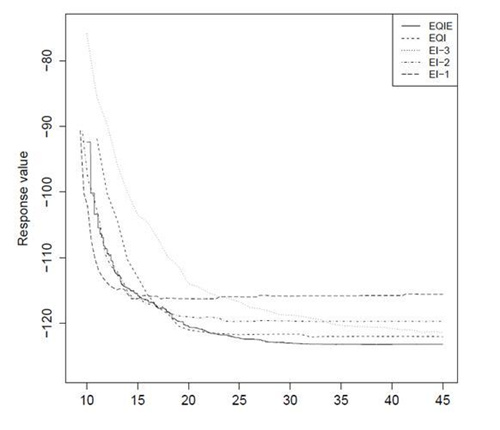
下图中我们通过数值结果来比较使用EI、EQI及EQIE的方法。EI方法使用单精度的实验,其中EI-1使用低精度实验,EI-2使用中精度实验,EI-3使用高精度实验。EQI则综合使用三种精度的实验,其中摸底实验采用80%的低精度实验及20%的高精度实验,追加实验则为高精度实验。EQIE的摸底实验精度与EQI相同,其追加实验的精度由EQIE判据得出,包含低、中、高、极高四种精度的实验。所有五种方法中,摸底实验都消耗9个单位的时间。随着追加实验不断增加,我们纪录由各个方法得到的推荐的输入值。根据这些输入值,我们计算出相应的精确解输出值。输出值越低,说明方法更好。下图中的五条曲线,即对应采用了五个方法后的输出值。图中的横坐标值,为已经使用的时间的总值。
可以看出,25个单位时间消耗后,EQIE是最好的方法,EQI其次,而三种EI方法均表现不佳。从EQI优于EI可以得到,追加实验的精度应高于摸底实验。从EQIE优于EQI看出,局部搜索实验的精度应高于全局探索性实验。此外,EI-2优于EI-1及EI-3,说明选取合理精度的重要性。采用EQIE方法后,由于使用了多精度实验,可以定量分析各种精度输出值与精确解的差距,从而采用整体合理的精度值。
我们将EQI及EQIE方法应用于某合金铸造模拟实验中,验证了方法的有效性。