科学研究和工程应用中的许多问题可以转化为含参数的代数方程组的求解问题。如几何定理的机器证明和自动发现，计算机视觉中著名的P3P问题，计算机程序的正确性验证等。对于参数多项式方程组求解问题，我们想知道对于什么样的参数取值，方程组有公共解。如果存在公共解，我们想进一步知道解的结构（有限组解，无穷组解，解的维数等等）。

解决这些问题的关键是要计算参数多项式系统的参数Groebner基:全局Groebner系统和全局Groebner基。

针对含参数的多项式理想，1992年德国学者Weispfenning提出了全局Groebner系统和全局Groebner基的概念，并给出了相关的计算方法。相关算法虽然可行，但是算法效率不高严重地制约了参数Groebner基的应用。为了提高算法的效率，参数Groebner基在国际上被广泛研究。除了Weispfenning领导的研究小组，美国学者Kapur，日本学者Sato，以及西班牙学者Montes等对参数Groenber基进行了深入的研究。

近年来，先进制造部王定康和合作者提出了一个计算全局Groenber系统的高效算法。在此基础上，他们又提出了一个同时计算全局Groebner系统和全局Groenber基的方法。这些算法已经在计算机代数系统中实现，需要者可从http://www.mmrc.iss.ac.cn/~dwang/software.html下载。相关算法到目前为止仍然是最为高效的，因此西班牙学者Montes将相关算法也在他自己Singular软件包grobcov.lib中加以实现(http://www-ma2.upc.edu/~montes/)。

王定康还成功地将参数Groebner基应用于几何定理的机器证明与自动发现。来源于计算机视觉中P3P问题也可以用参数Groebner系统自动求解。

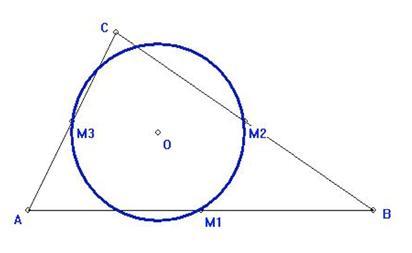
什么时候顶点A位于由三角形的三条边的中点所决定的圆的圆周上？