局部修复码是近几年的一个非常热门的研究方向，主要研究在分布式数据存储系统中通过局部修复提高存储节点修复效率的编码理论和方法。一些大型公司，如Microsoft，Facebook等已经在实际平台上运用了相关的编码技术。2012年Gopalan等人得到了关于局部修复码的极小距离的第一个Singleton型上界。由于码的极小距离是决定码的容错能力的重要参数，进而对刻画系统的可靠性起到关键性作用，因此确定局部修复码的最优极小距离成为分布式存储编码领域的一个重要问题。Gopalan等人的这篇先导性文章获得了2014年IEEE的通信领域和信息论领域的联合最佳论文奖。

随后的大批学者对该问题展开了一系列深入的研究。在2013年Tamo等人和Silberstein等分别利用Reed-Solomon码和Gabidulin码构造了r+1整除n时达到Gopalan等人界的最优局部修复码，但是用到的有限域大小关于n是指数的。2014年的一个重要进展是Tamo和Barg利用特殊多项式插值在和n差不多大的有限域上构造了最优的局部修复码，他们的文章获得了2015年IEEE信息论领域的最佳论文奖。

但是，一个重要问题是Gopalan等人的界在r+1不整除n的很多情形下是达不到的。2014年Song等人以及Prakash等人相继部分地改进了Gopalan等人的界，然而他们的结果对参数仍有过多的限制，或者无法得到一般的显式表示。

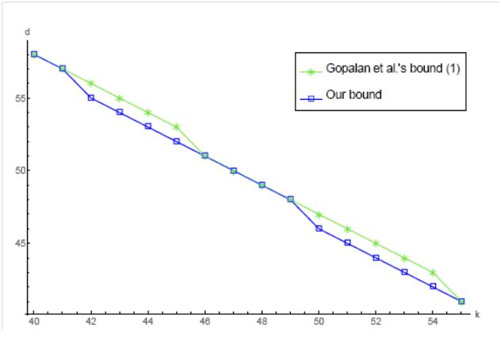
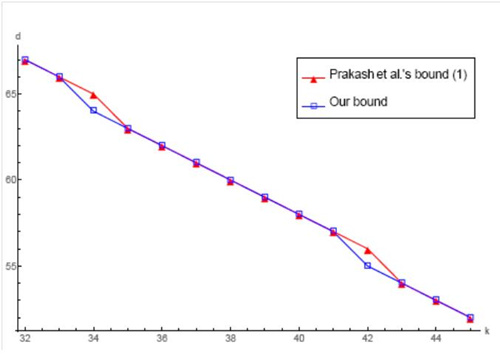
信息技术部的张志芳取得的重要进展是得到了参数n1>n2下（涵盖了实用的参数范围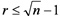）局部修复码的最优极小距离，也就是说，他们改进了之前Gopalan等人以及Prakash等人的上界，并且通过给出具体的最优码的构造说明了我们的界已经是紧的了。从而，完全确定了这一大类参数范围内局部修复码的最优极小距离。他们的参数范围不依赖于参数k，因此极大地扩充了Song等人的研究结果。例如，在下面的图中分别给出参数n=101,r=9时我们的界与Gopalan等人界和Prakash等人界的比较。

他们的这一结果目前已经发表在信息论领域权威期刊 IEEE Transactions on Information Theory.