2019-08-30 | 编辑：文/材料环境部

大规模稀疏线性代数方程组的快速求解是很多科学与工程计算软件的核心问题之一。代数多重网格（algebraic multigrid method或AMG）方法是一种求解一大类偏微分方程离散代数系统的高效算法。由于AMG具有较高的普适性、易用性和有效性，而且可以用于求解无结构网格问题，它们被广泛地应用于科学与工程计算中，已经成为很多商业工程计算软件的计算内核。

插值算子（或提升算子）的构造是AMG方法最重要的组成部分（图1）。在多重网格法收敛性理论中，著名的Xu-Zikatanov恒等式（XZidentity）于2002年发表在Journal of the？American Mathematical Society上。通过极小化XZ恒等式，可以得到最优的插值算子。但最优插值算子由对应于小特征值的广义特征向量构成的，计算代价太大。2004年，多重网格法领域国际知名专家R.Falgout和P.Vassilevski在SIAM Journal on Numerical Analysis上撰文提出了刻画“粗网格质量”的一种度量；通过极小化该度量，可以得到具有拟最优性的理想插值算子，该算子可以保证两网格方法的一致收敛性。相对于最优插值，理想插值的结构更简单且更易于实际计算。但一直没有理想插值算子的完整理论，传统观点认为：理想插值算子是唯一的和稠密的。

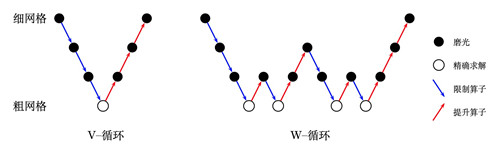
图1. 多重网格法的多层迭代过程，其中红色箭头表示插值算子或提升算子

近期，材料环境部张晨松副研究员及其博士生徐雪枫发现文献中对理想插值算子的这个认识有很大偏差，并分析给出了理想插值算子的一个充要条件[1]，该理论证明了理想插值算子是不唯一的，而且有可能设计出稀疏的理想插值算子，这为设计AMG算法提供了新的方向和动力。文章[1]还给出了一类理想插值算子的显式表达式，可以将许多AMG方法纳入到一个统一的框架下进行分析和比较，并给出了理想插值算子和最优插值算子之间的定量关系，理想插值算子可以看成最优插值算子的一种“松弛”。该项工作发表在计算数学领域国际顶级期刊SIAM Journal on Numerical Analysis上，徐雪枫因此工作获得“2018年北京计算数学学会优秀青年论文一等奖”。

参考文献：

［1］X. Xu and C.-S. Zhang. On the ideal interpolation operator inalgebraic multigrid methods. SIAM J. Numer. Anal., 56:1693-1710, 2018.