2019-12-10 | 编辑：文/材料环境部

两相流的移动接触线是流体力学中悬而未决的问题之一。 图1是一个两相流接触线的示意图。 两种流体（液体或者气体）形成的界面同固壁的交线在非平衡态下会移动,称为移动接触线。在移动接触线附近,使用经典的无滑移边条件会产生无穷大的能量耗散，物理学界称之为接触线悖论(moving contact line paradox)。悖论产生源自于此问题的本质多尺度属性。为避免接触线悖论，必须考虑接触线附近流体相对固体边界的微观滑移。为了在连续介质力学范畴内考虑微观滑移效应，许多边界条件模型被提出，其中基于相场模型的广义Navier滑移边条件(Qian, Wang and Sheng, Phy.Rev. E, 2003)因为能准确刻画分子动力学模拟结果，以及具有物理的变分结构而被广泛应用。但是相场模型因为存在一个界面厚度小参数，现在的计算机模拟能力很难达到小参数实际的物理尺度大小，因此一些物理学家仅仅把其当作现象学模型使用。另一方法，工程中实际使用的很多两相流模型属于尖锐界面(sharp-interface),实际计算时虽便于处理大尺度问题，但这些模型一般很难满足物理的变分结构，不容易处理存在复杂拓扑变化的情况。因为接触线问题在流体，材料和工业制造中的广泛性， 关于接触线理论和数值方法的研究一直是物理和交叉学科的一个重要研究方向(Bonn, Egger et al, Rev. Mod. Phys. 2009, Snoeijer and Andreotti, Ann. Rev. Fluid Mech. 2013)。

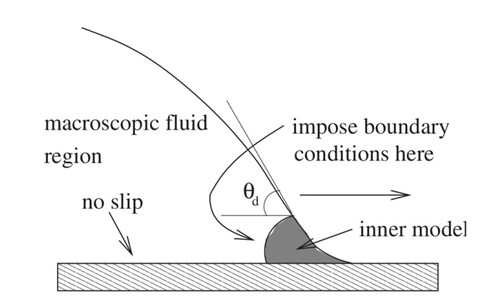
图1 移动接触线示意图(Bonn et al, Rev. Mod. Phys. 2009)

材料环境部的于海军、邸亚娜、许现民等人近几年对两相流接触线问题进行了系统的研究。

首先在数值方法方面， Qian-Wang-Sheng模型是一个Navier-Stokes流场方程和Cahn-Hilliard相场方程耦合的复杂非线性系统。因为模型的非凸性质和物理小参数的存在，非常难于计算。他们从方程的变分结构出发，设计了大步长下也能严格保证能量耗散的显隐数值离散格式。相关文章发表在国际权威期刊Journal of Computational Physics上[1]。 近期他们又同合作者一起设计了具有高阶时间离散精度的大步长下能量稳定的数值格式[2]。 这些工作发表之后得到了国际学者的广泛关注,引发了很多相关工作。

在模型方面，他们同合作者一起使用变分方法将Qian-Wang-Sheng模型推广到了两种流体具有不同密度和粘性的情形，得到了热力学相容的变密度两相流接触线模型，并设计了相应的保持能量耗散结构的无条件稳定数值离散格式，验证了模型在大密度比率情况下的适用性[3]。

他们也对相场接触线模型与尖锐界面模型之间的关系问题进行了研究。通过渐近分析和数值模拟，我们发现对相场模型中的几个现象学参数按不同的尺度规律设定，广义滑移边条件相场模型可以收敛于不同的尖锐界面模型。 经典的尖锐界面模型中使用的Jacqmin 2000边界条件， Spelt 2005条件， Gerbeau-Lelievre 2009边界条件等都可以从他们的分析中导出。通过使用前述构造的高阶数值格式，他们数值验证了相场方程关于界面参数的快速收敛特性，说明相场方程可以在界面参数取适中大小的时候得到可信的物理结果。这个工作发表在流体力学顶级期刊Journal of Fluid Mechanics上[4]。 该结果不仅可用来理解相场模型和明锐界面模型之间的关系，而且对数值计算中的参数选择具有重要指导意义。

参考文献:

[1] J.Shen(#), X. Yang, H. Yu(*), Efficient energy stable numerical schemes for a phase field moving contact line model, Journal of Computational Physics, 284:617-630, 2015

[2] X. Yang(#) and H. Yu(*), Efficient second order unconditionally stable schemes for a phase field moving contact line model using an invariant energy quadratization approach, SIAM Journal on Scientific Computing, 40(3):B889-B914, 2018

[3] H. Yu(#) and X. Yang(*), Numerical Approximations for a phase-field moving contact line model with variable densities and viscosities, Journal of Computational Physics, 334:665-686, 2017

[4] X. Xu(#), Y. Di and H. Yu(*), Sharp-interface limits of a phase-field model with a generalized Navier slip boundary condition for moving contact lines, Journal of Fluid Mechanics, 849:805-833, 2018